Возможности использования элементов теории вероятностей и статистики на уроках математики в начальной школе

.

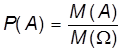Пример. Пусть событие A — выпадание на кубике четного числа; M(A) = 3. Здесь — множество всех возможных выпаданий; M() = 6. Значит, .

Пример. Возьмем мешок с 10 шариками (4 красных, 3 желтых, 3 синих). Ты наугад вынимаешь из мешка шарик. Множество элементарных событий состоит из 10-ти элементов; каждый элемент — вынимание одного шарика (M() = 10). Множество элементарных событий разбито здесь на три подмножества: красное (M(K) = 4), желтое (M(Ж) = 3), синее (M(С) = 3). Вероятность вытянуть с закрытыми глазами синий шарик определяется по формуле:

.

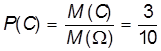Аналогично без труда находятся вероятности P(K) и P(Ж).

Пример. Возьмем колоду игральных карт. Элементарное событие — вытягивание карты из колоды. Всего карт 36: . Изобразим множество в виде таблицы:

Òàáë. F

Укажи меры следующих подмножеств:

– всех пиковых карт;

– всех дам;

– всех карт с картинками (валеты, короли, дамы).

Зная меры указанных подмножеств, определи вероятности вытянуть пиковую карту, вытянуть даму, вытянуть картинку.

По-видимому, для множеств с конечным числом элементов, где мера — число элементов, все ясно.

Можно было вести речь и о несчетных множеств, но нам кажется, что в начальной школе достаточно и этого материала.

Глава III. Анализ эксперимента

Как воспринимают школьники самые простые (или более сложные) задачи, направленные на активизацию различных мыслительных операций? Возможно ли научить учащихся начальных классов решать задачи и проводить эксперименты по теории вероятностей? Развиваются ли при этом мыслительные способности?

Чтобы ответить на эти вопросы, нами был проведен в гимназии № 1 г. Слонима. В эксперименте принимали участие ученики третьих классов. Эксперимент состоял из трех частей.

Констатирующий. Были предложены простые задачи для проверки восприятия школьниками вероятностных задач.

Методический (обучающий). Предлагалась система задач с использованием элементов теории вероятностей и статистики, которые они выполняли под руководством учителя, а также были даны первоначальные представления о теории вероятностей.

Контрольный. В этой части ученики решали задачи, похожие на задания из констатирующего эксперимента, но более сложного уровня для окончательной оценки умения решать логические задачи с элементами теории вероятностей.

III.1. Констатирующий эксперимент

Предложены следующие задания.

1. Есть 5 зрелых и 4 незрелых арбуза. Сколько арбузов надо купить, чтобы среди них был хотя бы один зрелый?

2. Есть три ключа от трех замков. Они перемешались. Сколько проб достаточно, чтобы подобрать ключи к замкам?

3. В аквариуме 6 золотых рыбок и 2 незолотые рыбки. Наугад достали 3 рыбки. Какие рыбки могли достать?

4. В мешочке 3 красных и 3 желтых шарика. Сколько надо вынуть наугад, не глядя в мешочек, шариков, чтобы быть уверенным в том, что:

а) хотя бы один из вынутых шариков будет красным;

б) два шарика будут разного цвета;

в) не будет ни одного красного шарика.

5. В мешочке 10 одинаковых по размерам и весу шаров, из которых 4 красных и 6 голубых. Из урны извлекается 1 шар. Какова вероятность (шанс) того, что извлеченный шар окажется голубым? Сколько нужно сделать попыток, чтобы достать 1 голубой шар?

Цель констатирующего эксперимента: проверить, как ученики III класса будут воспринимать и решать эти задачи, т. е. изучить начальный уровень знаний, умений, навыков.

Вывод. Результат констатирующего эксперимента освещен в таблице.