Математические модели в образовании

Рассмотрение проблем, связанных с формализацией предметной области педагогики, возможно на основе общих этапов математического моделирования. В границах графового моделирования разработаны подходы к организации исследовательской деятельности педагогов: пути исследования учебной книги на полноту, разработки учебных пособий справочного характера, конструирование модели обучения по различным учебн

ым пособиям и словарям, а также комплекс алгоритмов, связанных с обучением группы. Все вышеперечисленные алгоритмы универсальны, т.е. не зависят от того, с какой предметной областью работает педагог, это следует из универсальности моделей, на основе которых они построены.

Следовательно, обобщение исторического опыта и использование методов математического моделирования в педагогических науках, классификации применяемых в педагогике методов математического моделирования, описание функций математических моделей в образовательном процессе демонстрируют эффективность применения методов математического моделирования в образовательном процессе.

Суть познавательного процесса заключается в построении образа изучаемого объекта учащимся. Фиксирование такого образа с его основными свойствами и отношениями удобнее выполнять в математической форме, используя структурные или функциональные модели.

Структурные (не метрические) модели не отображают чисто количественные зависимости между величинами, а фиксируют разнообразные структурные отношения между ними (иерархию ценностей или мотивов, предпочтения в социальной группе и т.п.). В дидактике они используются с целью анализа структур процесса обучения (логической структуры учебного материала, структур познавательной деятельности учащихся, дидактических структур урока и т.д.). Функциональные (метрические) модели применяются для описания динамики исследуемых процессов, предсказания происходящих в них изменений. Такие модели называют прогностическими (трендовыми). Они описывают различные взаимосвязи между величинами с помощью функций и предназначены для изучения не структуры систем, а характера их поведения.

Математические модели представляют собой многофункциональное дидактическое средство, способствующее решению разнообразных педагогических задач. Использование математических моделей способствует достижению не только образовательных, но и развивающих дидактических целей. Это говорит о том, что модели, связанные с конкретным содержанием учебного предмета, помогают его представить ярко, наглядно, соединив строгость научных рассуждений с научным анализом структур изучаемых процессов и явлений. Модели закономерностей процесса обучения позволяют управлять познавательной деятельностью учащихся, учитывая степень влияния различных факторов, определяющих ее успешность.

Применения математической модели для подготовки компетентного специалиста

В качестве условия применения математических методов с точки зрения совершенствования качества образования определено содержание и характер математического образования в педагогическом процессе и выделен принцип педагогико-прикладной направленности математического образования, который взаимодействует с принципом образовательного гуманизма и является одним из методологических принципов при анализе качества педагогической деятельности. Принцип педагогико-прикладной направленности позволяет обратить внимание на необходимость изучения педагогическими факультетами специального курса «Математическая теория педагогических исследований», который может входить в общий курс высшей математики для студентов нематематических специальностей.

Разработанная интегративная модель межпредметного комплекса «математикапедагогикакибернетика» позволяет реализовать указанное направление (рисунок 1)

Предлагаемая модель построена на основе объединения областей математики, педагогики и кибернетики, включая уровни интеграции учебного предмета, кафедры, области педагогических исследований и систему непрерывного образования. Способом реализации данной модели выступает указанный спецкурс. Модель поможет подготовить компетентного специалиста, владеющего математико-педагогическими методиками, коррекционно-прогностическими, развивающими технологиями обучения, где он способен грамотно оценить качество образовательного процесса.

Одним из важнейших направлений повышения качества образования является совершенствование средств, методов и приемов диагностики, поиск эффективных инструментариев для оценки качества тех явлений в педагогической практике, которые влияют на становление и развитие личности субъектов образования. В связи с этим актуальной является разработка методик применения математических методов в личностно-ориентированном образовании.

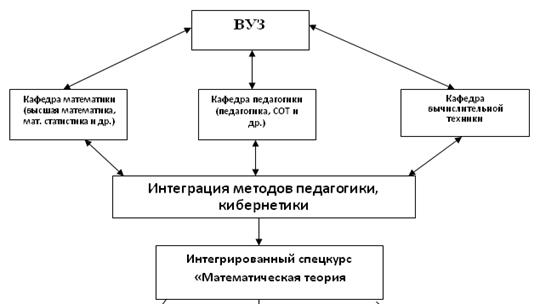
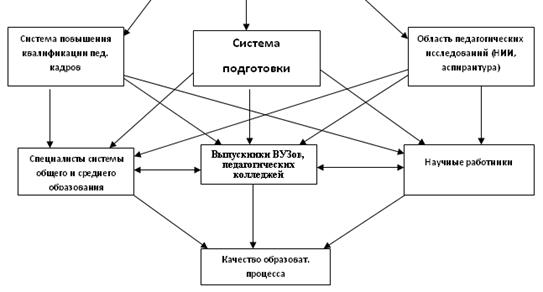
Рис. 1. Интегративная модель межпредметного комплекса «математикапедагогикакибернетика»

Построение формализованной математической модели оптимизации

В экспериментальной методике «Оптимизация учебного курса в личностно-ориентированном образовании» формулируется задача оптимизации курса определенного предмета для студентов высшего профессионального образования. Для построения формализованной математической модели оптимизации в виде системы ограничений и целевой функции был проведен опрос студентов нескольких групп. Был использован экспертный метод для учета возможностей и способностей этих студентов в приобретении знаний, навыков и умений на различных видах занятий (лекциях, практических, консультациях).

Полученные экспериментальные данные были приведены к норме относительно структуры действующего курса. Для этого рассмотрено действующее соотношение видов занятий курса: 32 лекции, 31 практическое занятие, 7 консультаций. Для данной разбивки часового фонда с учетом приведенных экспериментальных данных можно оценить среднюю информативность одного занятия каждого вида. В соответствии с принятым критерием оптимальности составлена целевая функция Z и ограничивающие условия:

Х10, Х20, Х30.

2,8Х1+0,2Х2+0Х3100

0Х1+1,1Х2+Х3100

0Х1+0,1Х2+1,5Х3100

Z=Х1+Х2+Х3max

Задача оптимизации свелась к стандартной задаче линейного программирования: определить значения неизвестных Х1, Х2, Х3, удовлетворяющие трем ограничениям и максимизирующие целевую функцию. Решение этой задачи осуществлялось симплекс-методом, одним из основных методов математического (линейного) программирования.