Разработка элективного курса "Физические основы теории протекания" для старших классов профильной школы

Процессы диффузии, такие, как распространение растворяемого вещества в растворителе или движение электронов в полупроводнике, ныне хорошо поняты.

Диффундирующая частица может достигать любой точки в среде. Иначе обстоит дело в случае протекания. Наиболее характерной особенностью перколяционных процессов является существование порога протекания, ниже которого процесс распространения жидкости

ограничен конечной областью среды. В качестве примера Бродбент и Хаммерсли рассмотрели распространение заболевания деревьев, при котором те сбрасывают листву и перестают расти, в саду, где деревья посажены в узлах квадратной решетки. Если расстояния между деревьями возрастают настолько, что вероятность заражения соседнего дерева падает ниже критического значения рс, то заболевание по саду не распространяется. Порогом протекания для этой задачи служит вероятность рс = 0,59275 для протекания от узла к узлу квадратной решетки. Другой пример-просачивание воды или радиоактивных отходов в трещины и разломы горной породы. Вопрос заключается в том, останется ли вода локализованной в каком-то объеме или будет распространяться все дальше и дальше. И в этой задаче можно ожидать, что существует критический порог концентрации трещин. Величину порога протекания можно определить с помощью численного моделирования. Аналогичной проблемой, имеющей огромный практический интерес, является распространение воды, вытесняющей нефть в пористых породах. В этом случае распространяющийся фронт жидкости (воды) может запереть нефть в некоторой области ("ловушке"), что приводит, как показали Уилкинсон и Виллемсен, к инвазивной перколяции. Случайность, связанная с инвазией (вторжением) вытесняющей жидкости, зависит, помимо прочего, от динамики образования ловушек. Идеи и понятия теории протекания применимы и к распространению и взаимосвязи трещин и разломов в горных породах и в материалах, используемых в технике.

Во многих приложениях не существует резкого различия между перколяционными процессами и диффузией. Важным случаем является диффузия от источника. Возникающий фронт диффузии имеет геометрическую структуру, тесно связанную с фрактальной геометрией протекания. На это впервые обратили внимание Саповал и др.

Задача о протекании допускает очень простое описание и приводит к множеству интереснейших фрактальных структур. Основные понятия теории протекания мы проиллюстрируем на примере двумерного протекания на квадратной решетке.

Бесконечный кластер при протекании

Как растет масса, или число узлов, М(L) наибольшего кластера с увеличением характерного размера L решетки? При р>рс мы ожидаем, что m(L)≈pn(p) L2, где правая часть при L→∞ стремится к Р∞(р)L2, а Р∞(р) есть просто плотность узлов, принадлежащих перколяционному кластеру. В то же время при р<рс мы ожидаем, что т(L)/L2→ 0 при L→∞, так как Р∞(р<рс) = 0. При р=рс можно ожидать, что М(L) будет возрастать почти как L2. Экстенсивные исследования зависимости M(L) от L привели к следующему результату:

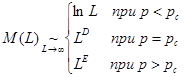(1)

Масса перколяционного кластера составляет при р>рс конечную долю всех узлов. Ниже рс кластер, простирающийся по всей решетке, как правило, не существует. Однако, если М(L) интерпретировать как размер Sмакс наибольшего кластера, то оказывается, что М(L) лишь очень слабо, т.е. логарифмически, возрастает с увеличением. На пороге протекания р=рс масса кластера, простирающегося по всей решетке (он является и наибольшим кластером), возрастает с увеличением L по степенному закону LD. Результаты численных экспериментов на квадратной решетке представлены на рис. 1.

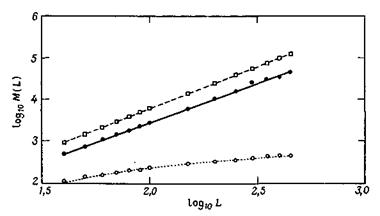
Рис. 1. Масса наибольшего кластера как функция линейного размера L квадратной решетки.

Черные кружки соответствуют р=рс=0,593. Сплошная линия-зависимость М(L)=ALD с D=1,89. При р=0,65 (светлые квадраты) кривая, проведенная через экспериментальные точки (штриховая линия), дает D = 2,03. При р = 0,5. т. е. при р < рс, экспериментальные точки (светлые кружки) ложатся на прямую M(L) = А + В In L (показанную пунктиром).

Они показывают, что перколяционный кластер на пороге протекания имеет фрактальную структуру с фрактальной размерностью D. Фрактальный перколяционный кластер на пороге протекания часто называют внутренним перколяционным кластером. Для результатов, представленных на рис. 1, фрактальная размерность D по оценкам имеет значение 1,89 + 0,03. Указанная ошибка имеет статистическую природу и характеризует качество подгонки степенного закона к результатам численного моделирования, представленным на рис. 1. Анализ систематических ошибок – дело тонкое. Когда перколяционный кластер на конечной решетке размером L составляет лишь часть внутреннего перколяционного кластера, то некоторые из узлов, не входящих в перколяционный кластер на решетке размером L, на самом деле принадлежат внутреннему перколяционному кластеру, так как соединены с ним связями, лежащими вне рассматриваемого фрагмента. При р>рс численное моделирование на квадратной решетке приводит к фрактальной размерности d= 2,03 + 0,01 для перколяционного кластеpa. И в этом случае ошибка имеет статистическую природу, a D есть угловой коэффициент прямой, проведенной через точки, полученные с помощью численного моделирования при р=0,65 и представленные на рис. 1. По точкам, соответствующим на этом рисунке наибольшим кластерам, была построена подгоночная прямая М(L) = А + В ln L с В=-426 и А = 327. Она проведена на рис. 1 штриховой линией. Все результаты численных экспериментов, представленные на рис. 1, согласуются с асимптотическим поведением, описываемым соотношением (1).

Сайкес и Эссам показали, что порог протекания от узла к узлу на треугольной решетке равен рс = 1/2 (точный результат). Это позволяет получать результаты для внутренних перколяционных кластеров с очень малой погрешностью, производя численные эксперименты на треугольной решетке. Такие результаты, полученные Штауффером [5] и представленные на рис. 1, позволяют получить для фрактальной размерности D оценку, согласующуюся с точным значением D = 91/48. Как показывают результаты численных экспериментов, это значение возникает в задачах с протеканием от узла к узлу на всех двумерных решетках.

Мы заключаем, что при протекании от узла к узлу на двумерных решетках внутренний перколяционный кластер имеет фрактальную структуру, и с увеличением L масса такого кластера возрастает в среднем как

M(L)~ALD, D = 91/48 = 1,895 . .(2)

Среднее берется по многим реализациям внутреннего перколяционного кластера. Амплитуда А есть эффективная амплитуда, вычисленная по значениям амплитуд для кластеров конечных размеров. Степенной закон (2) для массы внутреннего перколяционного кластера выполняется только асимптотически при больших L. При реалистических значениях L это скейлинговое соотношение следует модифицировать, введя в него поправочные члены: