Методика изучения алгебраических функций в восьмилетней школе

Для того чтобы изучить класс линейных функций в совокупности его общих свойств, необходимо поставить новую для учащихся познавательную задачу: исследовать класс функций у=kх+b в зависимости от параметров, установить геометрический смысл параметров. Эта задача возникает сразу же вслед за введением понятия функции. Наиболее естественный прием, который может быть применен, состоит в рассмотрении о

дновременно нескольких функций, у которых один из параметров изменяется, а другой остается постоянным. Простейшая система, реализующая этот прием, состоит из четырех заданий с их последующим анализом и установлением связей между ними.

Пример 5. Постройте графики функций:

у=0,5x; y=0,5x+0,5; y=1,5x; у=1,5x+0,5.

Основная часть работы начинается после построения графиков. Их нужно сравнить, обращая внимание на особенности графиков в зависимости от числовых значений коэффициентов. Опишем, например, методику выяснения геометрического смысла коэффициентов при переменной.

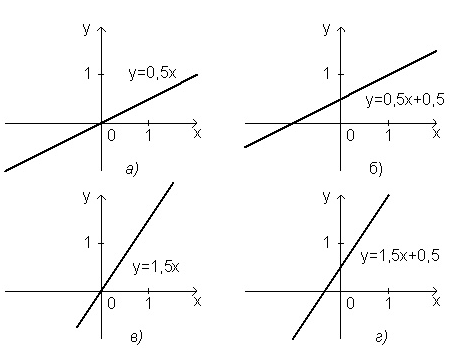
Рис 2.2.

Следует обратить внимание на то, что графики (а) и (б) образуют с осью абсцисс одинаковые углы, это же имеет место и для графиков (в) и (г). Кроме того, графики (а) и (б) образуют с осью абсцисс меньшие углы, чем (в) и (г). С другой стороны, коэффициенты при переменной в формуле для первой и второй функций одинаковы и меньше, чем соответствующие коэффициенты у третьей и четвертой функций. Можно после этого сформулировать вывод о зависимости рассмотренного угла от коэффициента, ввести термин «угловой коэффициент» и привести несколько закрепляющих упражнений.

Значительные трудности представляет случай отрицательных значений углового коэффициента; для него требуется отдельная работа, построенная аналогичным образом.

Приведём пример закрепляющего упражнения: на одном и том же чертеже изображены графики функций у =3x+2; у=3/4x+2.

Построить на этом же чертеже графики функций у = 3х—1;

у = 3/4х — 1; объяснить построение.

Если параметры, определяющие класс функций, имеют ясный геометрический смысл, то описанный прием изучения дает достаточно полное представление об этом классе. Однако в школьном курсе алгебры рассматриваются и такие классы, при изучении которых оказывается необходимым использовать и другие приемы.

Например, к изучению класса квадратичных функций привлекается прием, основанный на преобразовании выражения, задающего функцию, к виду а (х — b)2 + с, использовании геометрических преобразований для построения графика произвольной квадратичной функции из параболы стандартного положения — графика функции у=ах2, а≠0.

Остановимся на этом классе функций подробнее. Квадратичная функция вводится и изучается в тесной связи с квадратными уравнениями и неравенствами.

Первой из этого класса функций, в значительной степени еще вне изучения собственного класса, рассматривается функция у=х2. Свойства этой функции во многом отличаются от рассмотренного ранее случая линейных функций. Прежде всего, эта функция немонотонна; только на этом этапе у учащихся появляется пример функции, отличной от линейных, которые монотонны на всей области определения. Чтобы подчеркнуть указанное отличие, полезно предложить учащимся следующее задание: функция задана формулой у=х2 на промежутке -2≤х≤3. Найти множество значений этой функции. Перенося свойство монотонности с класса линейных функций на функцию у=х2, учащиеся часто делают ошибку, приводя ответ: промежуток 4≤x≤9. Эта ошибка для своего устранения требует рассмотрения графика функции у=х2.

Другое отличие состоит в том, что характер изменения значений функции у=х2 неравномерный: на одних участках она растет быстрее, на других — медленнее. Эта особенность выявляется при построении графика, причем целесообразно рассмотреть два графика: один — в крупном масштабе на промежутке,. -1≤x≤1, другой—в мелком масштабе на промежутке, например, -3≤х≤3. Построение можно вести описанным выше методом загущения. Важно отметить свойство параболы - симметричность относительно оси абсцисс; в дальнейшем это свойство приведет к рассмотрению класса четных функций, причем именно функция у = х2 будет ведущим примером функции этого класса.

Наиболее существенное применение, эта функция имеет при рассмотрении понятия иррационального числа. Первый пример иррационального числа (-√2) может быть введен различными способами, но независимо от этого необходимо объяснить его связь с графическим методом решения уравнения х2=2.

Изучение класса квадратичных функций начинается с изучения функций вида у=ах2; при этом выясняется геометрический смысл коэффициента а. Далее вводится более широкий класс функций, имеющий вид у=ах2+с. И здесь также коэффициент с получает ясную геометрическую интерпретацию, подойти к которой можно либо явно используя понятие параллельного переноса вдоль оси ординат, либо независимым рассуждением.

Пример 6. Задан график функции у=х2. Построить на этом чертеже график функции у=х2+1.

Заметим, что при заданном значении аргумента хо (рассматриваются, конечно, конкретные значения) значения функции у=х2+1 на одно и то же число, равное 1, больше значений функции у=х2. Поэтому для построения соответствующей точки на графике второй функции достаточно поднять на 1 точку графика первой функции с абсциссой Хо. Следовательно, чтобы построить весь график второй функции, нужно поднять на 1 график первой.

Это рассуждение хорошо усваивается учащимися, целесообразно применить его и при изучении класса линейных функций. В дальнейшем при обобщении свойств графиков его можно сформулировать так: «Чтобы построить график функции у=f(x)+с по известному графику функции у=f(х), можно произвести параллельный перенос второго графика на с единиц вдоль оси ординат».

После этой подготовки, казалось бы, можно приступить к изучению графиков произвольных квадратичных функций. Но здесь возникает трудность: коэффициент при первой степени неизвестного не имеет для квадратичной функции у=ах2+bх+с достаточно простого геометрического смысла. Именно поэтому приходится идти обходным путем, следуя тем же преобразованиям, которые производились при выводе формулы решения квадратного уравнения, и вводить в рассмотрение новый подкласс квадратичных функций вида у=а(х-b)2. Объяснения при построении графиков здесь в целом могут быть такими же, как при рассмотрении функций вида у=x2+с, однако усваивается предлагаемый способ здесь с большим трудом, поэтому требуется достаточное количество упражнений для закрепления. После таких приготовлений построение графика, а также изучение его свойств происходят без принципиальных затруднений.

Отметим здесь один частный, но полезный прием, который состоит в использовании системы заданий, имеющих цель — дать представление о тех или иных чертах данной функции или целого класса без указания точного значения величин, связанных с рассматриваемым вопросом. Этот прием можно назвать качественным или оценочным исследованием функции. Приведем два примера, связанные с изучением квадратичных функций.