Методика организации коллективной формы учебной деятельности учащихся на уроках математики в средней школе

Построить обе диагонали квадрата. Зафиксировать одну из них. На какие части одна диагональ делит квадрат? (Два равных равнобедренных прямоугольных треугольника).

В каждом из двух прямоугольных равнобедренных треугольников построить все биссектрисы. Что такое биссектриса и как построить биссектрису перегибанием листа бумаги? Какую фигуру мы выделили внутри квадрата? (Ромб). В чем отличия ром

ба и квадрата?

Перевернуть квадратный лист бумаги и построить линии, проходящие через вершину ромба, отличную от вершины квадрата, так, чтобы вершина квадрата, отличная от вершины ромба, попала на диагональ квадрата.

Согнуть лист по другой диагонали квадрата. Из каких многоугольников состоит получившаяся фигура? (Равнобокая трапеция и равнобедренный треугольник).

Отогнуть один равнобедренный треугольник по линии, проходящей через верхнее основание трапеции. Какая фигура получится из двух равных равнобедренных треугольников? (Ромб).

Для каждого из треугольников построить все биссектрисы и согнуть полученную фигуру по оси симметрии.

Фигура готова (рис. 8)!

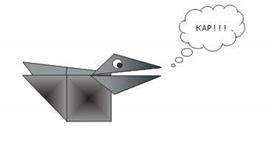
Рис. 8

Основной итог практической работы: с точки зрения оригами наиболее интересные линии в любом четырехугольнике – диагонали. С диагоналями чаще всего работаем при построении какой-нибудь фигуры. Результаты практических экспериментов заносим в таблицу (таблица 5). Приоритеты четырехугольников в оригами несколько отличаются от классического курса геометрии. Наиболее часто встречаются при построении квадрат, ромб и дельтоид.

Этот вид коллективной работы может быть прекрасно представлен на факультативном занятии по данной теме.

Таблица 5

При разработке фрагмента урока была использована следующая литература:

Фрагмент урока для 9-го класса по теме «Теорема синусов и теорема косинусов»

Комментарии к уроку

Тип данного урока систематизация и обобщение изученного материала. Его основная цель – систематизация знаний по пройденным темам.

В данном фрагменте представлен способ закрепления материала в форме коллективной деятельности.

Оборудование: сводная таблица.

Обобщение и систематизация изученного материала – 15 мин.

Коллективная работа в динамических парах. Ребята работают по двум блокам вопросов:

по теореме синусов;

по теореме косинусов.

Один учащийся из пары выполняет задания из первого блока, второй –из второго блока. Каждый заносит свой ответ в соответствующую колонку сводной таблицы (таблица 6), при необходимости можно использовать учебник. Затем ребята проверяют ответы друг друга, если находят ошибку записывают на их взгляд верное решение.

Итог работы класс подводит учитель вместе с учащимися по общей сводной таблице на доске.

Таблица 6

При разработке фрагмента урока была использована следующая литература:

Фрагмент урока для 9-го класса по теме «Теорема об отрезках хорд, пересекающихся внутри круга»

Комментарии к уроку

Данный фрагмент представляет собой пример того, как можно путем постановки проблемного домашнего задания создать на уроке ситуацию, побуждающую учащихся к анализу своих действий и самостоятельному выявлению нового материала. Тема урока заранее не объявляется, а вытекает из проблемной ситуации. Так, тема урока становится проблемой, разрешение которой увлекает учащихся.

Оборудование: доска, мел.

Изучение нового материала – 15 мин.

Перед изучением темы учащимися предлагается дома решить следующую задачу:

Хорда AB, пересеклась с хордой CD в точке О, делится на отрезки АО = 45 мм и ОВ = 30 мм. Определить отрезок CD, если OD = 90 мм.

Урок начинается с проверки выполнения домашнего задания. Выясняется, что большинство учеников справились с работой, притом различными способами.

Одни построили отрезок АВ = 75 мм, отметили на нем точку О и отложили отрезок OD = 90 мм по трем точкам A, B, D построили окружность. Точка С была найдена как точка пересечения прямой OD с этой окружностью.

Другие построили круг произвольного радиуса, в нем хорду АВ = 75 мм и на последней точку О. На окружности отметили точку D так, что OD = = 90 мм. Точка С была найдена как точка пересечения прямой OD с окружностью.

Третьи построили чертеж и нашли отрезок СО из подобия треугольников AOC и BOD.

Каждый способ решения задачи ученики объясняли по своим же чертежам. Последний способ решения задачи отмечается учителем как самый рациональный.

Учеников, вероятно, очень удивит то, что, несмотря на произвольность угла пересечения хорд (в первом случае), радиуса круга (во втором случае) и различия способов решения задачи, они получили один и тот же результат: СО = 15 мм. Это убедит их в существовании определенной зависимости между отрезками пересекающихся в круге хорд. Еще раз обратившись к третьему случаю решения задачи, ученики сформулировали проблему: найти свойство отрезков пересекающихся хорд. Затем учитель называет тему урока и записывает ее. Построив чертеж, ученики составляют пропорцию из отношения сходственных сторон подобных треугольников. Используя основное свойство пропорции, они дают формулировку теоремы.