Мысленный эксперимент в структуре геометрического доказательства

Такой подход Черняка к евклидовым «Началам» можно назвать «конструктивно-экспериментальным», где любое конструирование геометрической фигуры – есть мысленный эксперимент (см. введение, с.3). «Мысленный эксперимент имеет дело с идеализированными схемами эмпирического опыта, а его основной метод состоит в производстве различного рода вариаций, позволяющих мысленно обозреть все возможные случаи»–

пишет Черняк.

По его мнению, греки отвергли экспериментальный способ обоснования геометрии потому, что его идея была несовместима с духом греческой науки и философии. Ведь мысленный эксперимент подразумевает движение (в воображении), а оно: «…есть нечто вторичное, оно предполагает материю, хотя и «интеллигибельную»». Вычерчивание же линий на папирусе, песке или бумаге, есть уже чувственное подобие движения в фантазии.

Все что возникает подвержено изменению и исчезновению, а это противоречило представлениям греков о неизменности истинного знания. Воззрение древних было такого, что они презирали эксперимент и верили, что бытие можно познать посредством чистого мышления. «Посредством чувственного восприятия нельзя знать общее…ибо чувственно необходимо воспринимается отдельное, между тем как научное знание есть познание общего».

Исходя из выше изложенного, можно предположить, что мысленный эксперимент является своего рода «средой» существования геометрического объекта, где роль особых условий выполняют аксиомы, а внутренняя упорядоченность его «элементов» - роль системы связей. Конструирование геометрического объекта и оперирование с ним в такой «среде» ведет к открытию геометрического факта - теоремы.

В структуре геометрического доказательства практически всегда используются такие конструкции, как «дополнительные построения», выражаемые в словах типа: «проведем – достроим – поместим». После чего, используя дедуктивные рассуждения, выводится доказываемый факт. В таких «дополнительных построениях» по сути, свернут акт мысленного эксперимента, позволяющего схватить идею открытия теоремы, а значит и идею доказательства.

В современных учебниках по геометрии (Погорелов, Атанасян) идеи таких «дополнительных построений» не раскрываются, а их необходимость понимается лишь только тогда, когда доказательство теоремы завершено.

«Сконструировав» открытие теоремы как некоторого мысленного эксперимента с геометрической фигурой и изложив ее доказательство с использованием выделенной Библером, и отмеченной Давыдовым, структуры мысленного эксперимента, мы предполагаем, что у школьника может произойти оформление «для себя» идеи формально-дедуктивного доказательства теоремы.

Таким образом, мысленный эксперимент получает статус метода открытия геометрических теорем, позволяющий схватить в целом идею открытия. Последующее же формально-дедуктивное доказательство уже не представляется чем-то «туманным» и не очень понятным. Оно необходимо для избежания наглядно-чувственного восприятия доказательства теоремы и его идея содержится в ее «открытии», в ее «конструировании» как мысленного эксперимента с идеальной геометрической фигурой.

Теорема о средней линии трапеции

Рассмотрим теорему о средней линии трапеции. Эта теорема по-разному представлена в школьных учебниках геометрии под авторством Погорелова А.В. и Атанасяна Л.С. В учебнике Атанасяна Л.С. теорема доказывается через понятие вектора, а точнее через правило построения суммы нескольких векторов, называемое правилом многоугольника. Рассмотрим доказательством этой теоремы, приведенной в учебнике А.В. Погорелова, поскольку она доказывается с помощью дополнительного построения, и в этом смысле более «просто» и схоже с евклидовым. Приведем его дословно:

«Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Определение трапеции: трапеция - это четырехугольник, у которого только две противолежащие стороны параллельны.

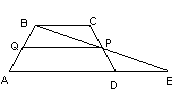
Доказательство. Пусть ABCD – данная трапеция. Проведем через вершину В и середину Р боковой стороны CD прямую. Она пересекает прямую AD в некоторой точке Е.

Треугольники PBC и PED равны по второму признаку равенства треугольников. У них CP=DP по построению, углы при вершине Р равны как вертикальные, а углы РСВ и PDE равны как внутренние накрест лежащие при параллельных прямых ВС и АD и секущей СD.

Из равенства треугольников следует равенство сторон: РВ=РЕ, ВС=ЕD. Значит, средняя линия PQ трапеции является средней линией треугольника АВЕ. По свойству средней линии треугольника PQ || AE и отрезок PQ=1\2AE=1\2*(AD+BC). Теорема доказана».

Такое доказательство не позволяет «понять», откуда берется идея построения линии ВЕ. Тогда как именно в проведение этой линии и свернут акт мысленного эксперимента. Ведь после такого «дополнительного построения» остается лишь доказать равенство нужных треугольников. Наша задача состоит в «реконструкции» мысленного эксперимента как важного компонента доказательства.

Доказательство теоремы с использованием мысленного эксперимента.

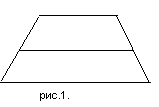
Итак, предмет мысли нашего мысленного эксперимента – отрезок, соединяющий середины боковых сторон трапеции с ее основаниями, т.е. средняя линия трапеции (рис.1.). Но мы не сможем что-либо узнать об этом отрезке, пока он находится в условиях трапеции. Мы должны поместить его мысленно в такие условия, в которых его сущность может раскрыться с особой определенностью (1этап).

Такими условиями является наделение одной из боковых сторон трапеции следующими идеальными свойствами:

- боковая сторона трапеции способна сжиматься и растягиваться, сохраняя при этом прямизну линии;

- точки боковой стороны, соприкасающиеся с основаниями, способны скользить по прямым линиям, содержащим основания трапеции. При этом точка, являющаяся серединой боковой стороны не должна менять своего расположения (т.е быть центром скольжения).

Такие сконструированные условия позволяют нам раскрыть сущность средней линии трапеции с особой определенностью (1 этап) – быть параллельной ее основаниям.

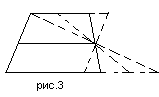
В самом деле: проводя последующие мысленные трансформации (2 этап) путем «вращения» идеализированной боковой стороны, мы будем получать различные варианты четырехугольника, с двумя параллельными сторонами, стремящегося в предельном случаи (совмещении двух вершин) к треугольнику (рис.3), где средняя линия трапеции сохраняет свойство быть средней линией получаемых фигур. Трансформация средней линии трапеции заключается в том, что она перестает быть средней линией трапеции, становясь средней линией другого геометрического объекта – треугольника.

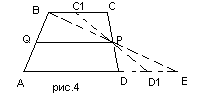
Производя обозначение вершин трапеции, треугольника, средней линии (рис.4), мы тем самым мысленно формируем ту среду, ту систему связей, в которую помещаем наш предмет мысли (3 этап).