Методика изучения свойств прямоугольного треугольника в курсе геометрии 7-8 классов

В главе 2 представлены методические рекомендации для изучения данной темы, характеристика возрастных особенностей учеников 7- 8 классов, что позволяет учителю правильно строить уроки; разработаны некоторые примерные уроки по данной теме.

Практическая значимость работы заключается в том, что данный материал может быть использован студентами педагогических Вузов для работы на лабораторных зан

ятиях по методике преподавания математики, а также работа будет интересна начинающим специалистам некоторыми своими методическими рекомендациями.

Введение понятия прямоугольного треугольника

Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – сторонами.

На рисунке 1 мы видим треугольник с вершинами A, B, C и сторонами AB, AC, CB.

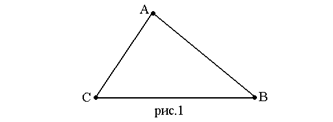
Треугольник обозначается указанием его вершин. Вместо слова «треугольник» иногда употребляют знак Δ. Например, треугольник на рисунке обозначается так: Δ ABC. Три угла- Ð BAC, ÐCBA, ÐACB – называют углами треугольника ABC. Часто их обозначают одной буквой ÐA, ÐB, ÐC.

Треугольник называется прямоугольным, если у него есть прямой угол. Стороны прямоугольного треугольника имеют специальные названия:

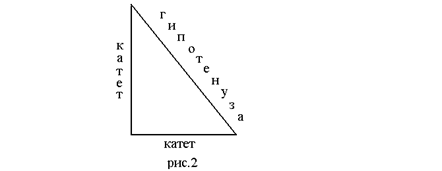
гипотенуза – сторона, лежащая против прямого угла; катеты – стороны прилежащие гипотенузе (рис. 2).

Так как сумма углов в треугольнике равна 180˚, то у прямоугольного треугольника только один прямой угол. Два другие угла прямоугольного треугольника – острые. Сумма острых углов в прямоугольном треугольнике равна 180º – 90º = 90º.

Утверждение. В прямоугольном треугольнике гипотенуза больше катета.

В самом деле, гипотенуза лежит против прямого угла, а катет, против острого. Так как прямой угол больше острого, то гипотенуза больше катета.

Прямоугольный треугольник и его свойства

Рассмотрим свойства прямоугольных треугольников, которые устанавливаются с помощью теоремы о сумме углов треугольника.

В прямоугольном треугольнике гипотенуза больше катета (следствие из теоремы о соотношении между сторонами и углами в треугольнике).

1°. Сумма двух острых углов прямоугольного треугольника равна 90°.

В самом деле, сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника равна 90°.

2°. Катет прямоугольного треугольника, лежащего против угла в 30º, равен половине гипотенузы.

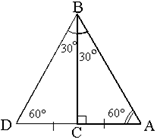
Пусть ABC – прямоугольный треугольник с прямым углом C и углом B равным 30º, а значит, угол A равен 60° (рис. 3). Построим треугольник DBC равный треугольнику ABC, как показано на рисунке. У треугольника ABD все углы равны (60º), поэтому он равносторонний.

Так как AC=AD, а AD=AB, то AC=AB.

Что и требовалось доказать.

3°. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30º (обратная теорема).

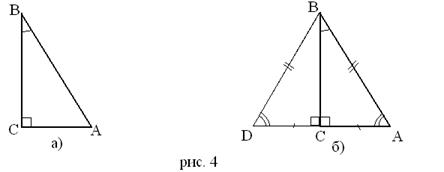
Рассмотрим прямоугольный треугольник ABC, у которого катет AC равен половине гипотенузы AC (рис. 4 а). Докажем, что <ABC = 30°.

Приложим к треугольнику ABC равный ему треугольник DBC так, как показано на рисунке 4 б). Получим равносторонний треугольник DBA. Углы равностороннего треугольника равны друг другу, поэтому каждый из них равен 60°. В частности < DBA=60°. Но <DBA=2<ABC. Следовательно, <ABC=30°.

Что и требовалось доказать.

Признаки равенства прямоугольных треугольников

Чтобы установить равенство прямоугольных треугольников, достаточно знать, что два элемента одного треугольника соответственно равны двум элементам другого треугольника (исключая прямой угол). Это, конечно, не распространяется на равенство двух углов одного треугольника двум углам другого треугольника.

Так как в прямоугольном треугольнике угол между двумя катетами прямой, а любые два прямых угла равны, то из первого признака равенства треугольников следует:

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны (рис 5).

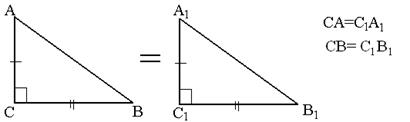
Далее, из второго признака равенства треугольников следует:

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему углу другого треугольника, то такие треугольники равны (рис. 6).

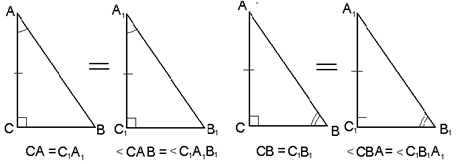
Рассмотрим ещё два признака равенства прямоугольных треугольников.

Теорема. Если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого треугольника, то такие треугольники равны (рис. 7).

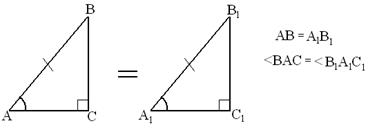
Доказательство. Из свойства 1º §2 следует, что в таких треугольниках два других острых угла тоже равны, поэтому треугольники равны по второму признаку равенства треугольников, то есть по стороне (гипотенузе) и двум прилежащим углам.

Что и требовалось доказать.

Теорема. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.

Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых углы C и C1 – прямые, AB =A1B1, BC = B1C1 (рис. 8).

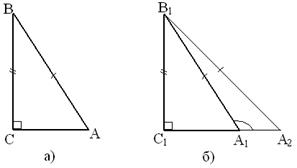
Так как < C = < C1, то треугольник ABC можно наложить на треугольник A1B1C1 так, что вершина C совместится с вершиной C1, а стороны CA и CB наложатся соответственно на лучи C1A1 и C1B1, поскольку CB = C1B1, то вершина B совместится с вершиной B1. Но тогда вершины A и A1 также совместятся. В самом деле, если предположить, что точка A совместится с некоторой другой точкой A2 луча C1A1, то получим равнобедренный треугольник A1B1A2, в котором углы при основании A1A2 не равны (на рисунке < A2 – острый, а < A1 - тупой как смежный с острым углом B1A1C1). Но это невозможно, поэтому вершины A и A1 совместятся. Следовательно, полностью совместятся треугольники ABC A1B1C1, то есть они равны.

Что и требовалось доказать.

Теорема Пифагора