Параллельные прямые в курсе основной школы

(2)

где q – та же постоянная, что и в формуле (1).

Круг при стремлении его радиуса к бесконечности переходит в системе Лобачевского не в прямую, а в особого рода кривую «предельного круга» - в настоящее время такие кривые называют орициклами. Сфера при тех же обстоятельствах переходит не в плоскость, а в кривую поверхность

, которую Лобачевский назвал «предельной сферой», а в настоящее время именуют орисферой. Лобачевский отмечает, что на орисфере имеет место евклидова геометрия, причем роль прямых на ней играют орициклы. Это позволяет Лобачевскому, опираясь на евклидову тригонометрию на орисфере, вывести тригонометрию на плоскости в его геометрической системе. Название «воображаемая геометрия» подчеркивает, что эта геометрия относится к евклидовой, «употребительной», по терминологии Лобачевского, как мнимые числа, «воображаемые», по его терминологии, к действительным.

Лобачевский сразу же поставил вопрос об экспериментальной проверке того, какая геометрия имеет место в реальном мире – «употребительная» или «воображаемая», для чего он решил измерить сумму углов треугольника, образованного двумя диаметрально противоположными положениями Земли на ее орбите и Сириусом и считая один из углов этого треугольника прямым, а другой – равным углу параллельности, Лобачевский нашел, что эта сумма отличается от на разность, меньшую ошибки угломерных инструментов в его время. «После того, - пишет Лобачевский, - можно вообразить, сколько эта разность, на которой основана наша теория параллельных, оправдывает точность всех вычислений обыкновенной геометрии и дозволяет принятые начала рассматривать как бы строго доказанными».

Это объясняет, что под «строгим доказательством теоремы о параллельных» в докладе 1826 г. Лобачевский понимал невозможность установить экспериментальным путем ,какая из двух геометрий имеет место в реальном мире, откуда вытекает, что на практике можно пользоваться «употребительной геометрией», не рискуя впасть в ошибку.

Наиболее полно изложена система Лобачевского в его «Новых началах с полной теорией параллельных» (1835-1838). Изложение геометрии у Лобачевского основывается на чисто топологических свойствах прикосновения и сечения, конгруэнтность тел и равенство отрезков определяются по существу с помощью движения.

В позднейших работах Лобачевский ввел координаты и вычислил из геометрических соображений целый ряд новых определенных интегралов, которым он специально посвятил работу «Применение воображаемой геометрии к некоторым интегралам» (Учен. зап. Казан. ун-та, 1836), многие из которых были включены в дальнейшие справочники.

Изучив теорию вопроса о параллельных прямых я узнала о том какие теории есть еще, т.е. Геометрии отличные от геометрии Евклида. Например, геометрия Н.И.Лобачевского, в его геометрии через точку не лежащую на данной прямой проходит бесконечно много прямых параллельных данной.

Оказалось что его геометрия не только не хуже евклидовой, но в некотором отношении даже совершеннее ее, богаче.

Геометрия Римана, в его геометрии прямые это замкнутые линии, на которых точки расположены как на окружности, только очень большого диаметра. В геометрии Римана не существует вообще никакой прямой , проходящей через данную точку параллельно данной прямой. Это второй вид неевклидовой геометрии.

Янош Больяи пытался доказать V постулат Евклида (аксиома параллельности), сохранившиеся чертежи свидетельствуют, что Больяи уже тогда был на пути к открытию неевклидовой геометрии, но его открытие записанное в «Аппендиксе» не было признано при его жизни.

А.М.Лежандр является автором школьного учебника «Начала геометрии», он переиздавался при жизни автора 14 раз. Объяснялось это тем, что каждый раз он обнаруживал ошибку в доказательстве V постулата. Однако его исследования очень поучительны и вскрывают глубокие связи между V постулатом и другими предложениями.

Методика преподавания темы «Параллельные прямые»

Параллельные прямые

К понятию о параллельных прямых следует подвести учащихся следующим образом. Учащимся предлагается провести произвольную прямую АВ, отметить на ней две близлежащие точки М и N, и провести через эти точки к прямой АВ перпендикуляры ММ1 и NN1. ставиться вопрос, пересекутся ли эти перпендикуляры, если их продолжить в ту или другую сторону от прямой АВ.

Если на заданный вопрос последует ответ, что прямые не пересекутся, а это учащиеся чувствуют интуитивно, или, наоборот, будет дан ответ, что прямые пересекутся, необходимо указать учащимся, что каждое из сделанных ими утверждений должно быть доказано, т.е. обосновано ссылками на известные им аксиомы и теоремы.

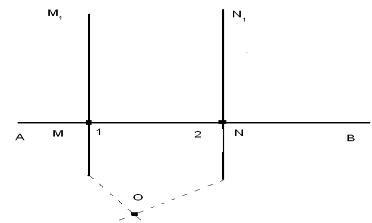
Доказательство: имеем ММ1 перпендикулярно АВ, NN1 перпендикулярно АВ. Докажем, что перпендикуляры ММ1 и NN1, проведенные к одной и той же прямой АВ, не могут пересечься. Предположим противное, а именно - что перпендикуляры ММ1 и NN1 пересекутся в некоторой точке О, тогда получиться треугольник МОN, в котором сумма внутренних углов 1 и 2, равна двум прямым: 1+2=180º, что невозможно, так как сумма двух углов треугольника всегда меньше 180º. Отсюда следует, что принятое допущение, что перпендикуляры ММ1 и NN1 при своем продолжении пересекутся в некоторой точке О, неверно. Итак, два перпендикуляра к одной и той же прямой не пересекутся, сколько бы их не продолжать.

После такого разбора учащимся указывается, что на плоскости можно расположить две прямые так, что они никогда не пересекутся, и дается определение: прямые, которые расположены в одной плоскости и не пересекаются, называются параллельными.

Возвращаясь затем к полученному выше выводу о взаимном положении двух перпендикуляров к одной и той же прямой, преподаватель отмечает, что этот вывод можно формулировать в виде теоремы: две прямые перпендикулярные к третьей, параллельны.

Вводится знак для обозначения параллельности двух прямых: АВ║CD.

Преподаватель должен подчеркнуть, что необходимым условием для параллельности двух прямых является то, что прямые должны лежать в одной плоскости. Это указание должно быть выявлено в определении, а потому определение параллельных прямых без слов « которые расположены в одной плоскости» является неполным.

Следует использовать модель куба для показа параллельных и непараллельных прямы.

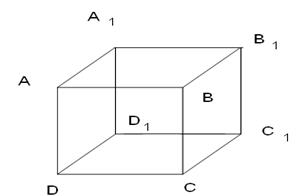
Так, ребра куба АВ и А1D1 не пересекаются: они лежат в разных плоскостях, поясняется, что такие прямые, в отличие от прямых параллельных, называются скрещивающимися.

Ребра же куба АВ и А1В1, АА1 и ВВ1, ВВ1 и СС1 также не пересекаются , однако они попарно расположены в одной плоскости, они параллельны.

Теорема о двух перпендикулярах на плоскости к одной и той же прямой является одним из признаков параллельных прямых. Необходимо показать учащимся ее практическое приложение, для чего следует решить задачу: На плоскости даны две точки А и В. Провести через эти точки две параллельные прямые.