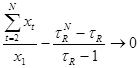Проведение статистического анализа и прогнозирование результатов выпуска изданий Беларуси и России
Прогноз рассчитывается по формуле:
|
|
(1.16) |
1.3.2. Метод скользящего среднего
Метод скользящего среднего основан на выравнивании ряда с использованием следующей формулы:
![]() ,
,
(1.17)
![]() ,
,
(1.18)
где ![]() — значение скользящего среднего в момент времени t;
— значение скользящего среднего в момент времени t;
![]() — некоторая величина, характеризующая начальное условие при
— некоторая величина, характеризующая начальное условие при ![]() ;
;
![]() — значение скользящего среднего в момент времени
— значение скользящего среднего в момент времени ![]() ;
;
N — число значений ряда.
1.3.3. Метод Брауна
Метод Брауна основан на использовании адаптивных моделей разного порядка. Адаптивные модели первого порядка основаны на использовании экспоненциальной средней, отличие состоит в выборе ![]() . Начальные условия для расчета:
. Начальные условия для расчета:
|
|
(1.19) |
где ![]()
![]() , где
, где
![]() — это шаг.
— это шаг.
Расчет производится по следующим формулам:
|
|
(1.20) |
|
|
(1.21) |
Прогноз следующего значения ряда вычисляется по следующей формуле:
|
|
(1.22) |
Для построения графических зависимостей пользуются столбцами значений: х и ![]() .
.
1.3.4. Метод среднего темпа
При использовании этого метода в расчете учитывается вся информация ряда. Расчет базируется на предпосылке о том, что сумма фактических уровней динамического ряда или суммарный рост за период должен быть равен сумме уровней, полученных расчетным путем исходя из начального уровня ряда и среднего темпа роста (![]() ).
).
Он производится по формуле:
|
|
(1.23) |
Расчет уровня ряда:
|
|
(1.24) |
где ![]() .
.
Расчет проводится путем подбора ![]() при соблюдении следующего условия:
при соблюдении следующего условия:
|
|
(1.25) |
Когда определено значение ![]() , при котором
, при котором ![]() , найденное значение среднего темпа роста выступает в качестве коэффициента для составления прогноза на будущий срок.
, найденное значение среднего темпа роста выступает в качестве коэффициента для составления прогноза на будущий срок.
Высчитывается по формуле:
|
|
(1.26) |
2. Статистический показатель расчетов
временных рядов (корреляция)
Случайной величиной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Случайная величина называется дискретной, если ее возможные значения можно пронумеровать. Основными формами задания дискретной случайной величины являются: 1) ряд распределения; 2) функция распределения (интегральная функция распределения).
Математическое ожидание дискретной случайной величины Х называется значение, рассчитанное по формуле
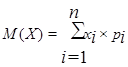 . (2.1)
. (2.1)
Математическое ожидание обозначается также mx. Оно приближенно равно среднему возможному значению случайной величины.
Случайная величина называется непрерывной, если ее возможные значения сплошь заполняют некоторый интервал. Основными формами задания непрерывной случайной величины являются:
· интегральная функция распределения F(x);
· функция плотности вероятности f(x).
Интегральная функция распределения для непрерывной случайной величины Х определяется так же, как и для дискретной F(x) = P(X < x).
Плотность вероятности (дифференциальной функцией распределения) случайной величины Х называется функция
f(x) = F´(x). (2.2)
Для непрерывной случайной величины Х функция распределения F(x) непрерывна на всей оси Ох, а плотность вероятности f(x) существует везде, за исключением, может быть, конечного числа точек.
Математическим ожиданием mx непрерывной случайной величины Х, для которого функция f(x) является плотностью вероятности, называется величина несобственного интеграла
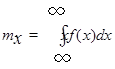 , (2.3)
, (2.3)
если он сходится.
Дисперсией называется значение несобственного интеграла
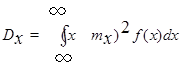 , (2.4)
, (2.4)
если он сходится.
При вычислении дисперсии иногда удобна формула
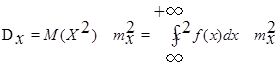 . (2.5)
. (2.5)
Кроме математического ожидания для характеристики положения центра распределения случайной величины часто используют моду и медиану. Модой называется то значение случайной величины, которому соответствует наибольшая плотность вероятности ее распределения.
Другие рефераты на тему «Журналистика, издательское дело и СМИ»:
Поиск рефератов
Последние рефераты раздела
- PR в государственных структурах на примере Воронежской областной администрации и Воронежской городской администрации
- Особенности интервью со звездой
- Особенности и специфика деятельности пресс-секретаря
- Освещение российскими СМИ ливано-израильского конфликта
- Авторская позиция как выражение субъективного начала в журналистском тексте (на материале красноярской прессы в период 1996-1998гг.)
- Вспомогательный справочный аппарат периодических изданий
- Анализ телеканала СТС

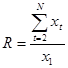 ,
,