Эвристические методы поиска способа решения задач

Для иллюстрации метода подходит следующая задача.

Задача 14. В четырехугольнике ABCD две стороны AD и BC не параллельны. Что больше: полусумма этих сторон или отрезок MN, соединяющий середины двух других сторон четырехугольника?

	"images/referats/12165/image082.png">

Поиск решения. Важно представить, что будет получено в предельном случае, когда В одна из сторон четырехугольника стянется в одну точку. В данном случае стягивать в точку МN можно либо BC (или AD), либо AB (или CD).

Рассмотрим первый случай, тогда пусть BC стянется в точку B. В предельном положении А D точка N совпадет с серединой К отрезка BD, и MN станет средней линией MK

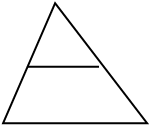Bтреугольника ABD, в предельном случае получаем такую задачу: что больше, половина стороны AD треугольника ABD или отрезок M, соединяющий MK (N)середины двух других сторон?

Ответ прост: MK = AD.

Поставим цель – свести к полученному предельному

ADслучаю решение задачи в общем случае.

Решение. Пусть К – середина диагонали BD четырехугольника ABCD. Из ABD имеем MK = AD и MK || AD. Также из BCD имеем KN = BC и KN || BC.

СТак как по условию AD и BC не параллельны, то Вточки M, K, N не могут находиться на одной прямой. Из MKN видно, что MN < MK+KN =

MN= (1/2)(AD+BC).

4.4 “Соображения непрерывности”

В математике часто заключения об истинности или правдоподобии какого-то факта выводятся с помощью соображений непрерывности. Несмотря на то, что для учащихся школы строгое определение непрерывности сложно, наглядное представление о величинах, меняющихся непрерывно с течением времени имеет каждый (например, путь, величина угла и т.д.).

Отправляясь от таких наглядных представлений, можно дать математическое определение того, что значит, какая-то величина U менялась с течением времени непрерывно: это значит, что при любом выборе момента tв течение достаточно малого промежутка времени (t-h, t+h) значения этой величины отличались от ее значения в момент tменьше, чем наперед заданное допустимое отклонение d. Следует иметь ввиду, что допустимое отклонение d задается здесь заранее и может быть выбрано как угодно малым. Утверждается, что при любом таком выборе d можно в зависимости от этого d для каждого момента tподобрать настолько малый промежуток времени (t-h, t+h), чтобы значения величины U в любой момент из этого промежутка отличались от его значения в момент tменьше, чем на d. В конкретных случаях обычно бывает достаточно ясно, можно ли считать, что та или иная величина меняется непрерывно.

При решении задач особенно полезно бывает следующее интуитивно очевидное свойство непрерывно меняющейся величины: если какая-либо величина (например, длина, сумма углов, площадь и т.п.) менялись непрерывно в течение какого-либо отрезка времени и в начальный момент она была меньше постоянной величины а, а в конечный момент больше, чем а, то в какой-то промежуточный момент она была равна а.

Применение данного свойства хорошо иллюстрирует следующий пример.

Задача15. Легко догадаться, что уравнение 2=4х имеет корень х=4. Имеет ли оно еще хотя бы один корень?

Решение. Рассмотрим “поведение ” этой функции на отрезке [ 0; 1].

При х= 0 2- 4х > 0, а при х= 1 2- 4х < 0, поэтому найдется такое промежуточное значение х, что 2- 4х = 0.

Заключение

В работе на основе изучения структуры решения математической задачи был выделен этап поиска решения задачи, который в случае решения нестандартной задачи выполняется, если используется применение эвристических приемов решения задачи.

Такое условие привело к необходимости изучения понятия эвристического метода и систем эвристических приемов решения математических задач Л.М. Фридмана и М.Б. Балка. Изучение и сравнение данных систем потребовало их изложения с приведением примеров математических задач с решениями в роли иллюстраций к особенностям каждой системы.

Литература

1. Балк Г.Д. О применении эвристических приемов в школьном курсе математики // Математика в школе. – 1969. – №5. – С.21–28.

2. Балк М.Б., Балк Г.Д. О привитии школьникам эвристического мышления // Математика в школе. – 1985. – №2. – С.55 – 60.

3. Большая Советская Энциклопедия, 1978. Том 29.

4. Пойа Д. Как решать задачу. – Львов: журнал “Квантор”,1991.

5. Фридман Л.М. Теоретические основы методики обучения математике в школе: Пособие для учителей, методистов и педагогических высших учебных заведений. – М.: Флинта, 1998.

6. Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи: Книга для учащихся старших классов средней школы. – М.: Просвещение, 1989.

7. Пушкин В.Н. Эвристика – наука о творческом мышлении. – М.: Политиздат, 1967.

 Скачать реферат