Расчет максимального значения восстанавливающей силы

- коэффициенты вязкого трения в опорах 7-9.

Потерями в опоре 9, массой вала «а» и податливостью вала «в» пренебречь.

Сателлит 2 совершает сложное движение: его абсолютное движение складывается из относительного – вокруг собственной оси и переносного – вращение вместе с водилом относительно оси вала «в». Пользуясь методом В

иллиса, определим направление переносного движения, т.е направление вращения водило. Допустим, что все звенья передачи 1,2,3 и 4 жестко соединены друг с другом. Сообщая этой жесткой системе переносное вращательное движение вокруг оси вала «в» с угловой скоростью равной скорости вращения водила, но обратно по знаку. При таком движении водило окажется остановленным , в результате относительные угловые скорости зубчатых колес 1 и 3 будут равны:

(1)

(2)

где абсолютные угловые скорости колес 1 и 3; относительные угловые скорости колес 1 и 3; скорость вращения водила.

При планетарная передача превращается в простую зубчатую передачу в которой оси всех зубчатых колес неподвижны.

Тогда передаточное отношение передачи будет иметь вид:

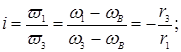(3)

Преобразуем данное уравнение:

А поскольку колесо 3 является неподвижным , то

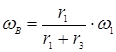(4)

Из (4) следует, что направление вращения водила совпадает с направлением вращения колеса 1, то есть скорости относительного и переносного вращения сателлита 2 противоположны по знаку.

Используя метод аналогий представим механическую систему в виде эквивалентных схем каждой из подсистемы (рисунок 3).

Запишем уравнения для источника :

,

где ;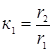

Запишем уравнение равновесия моментов:

;

,

Аналогично запишем уравнение для , , . Так,

,

где ;

Запишем уравнение равновесия моментов:

;

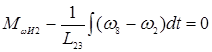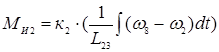(5)

Уравнение для :

, где ;

;

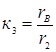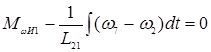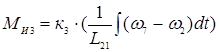. (6)

Уравнение для :

, где ;

;

.

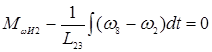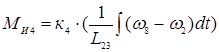Запишем уравнения для зависимых источников угловых скоростей:

,

где ;

=(7)

,

где ;

=

Составим уравнение равновесия в узлах эквивалентных схем.

1 подсистема:

узел 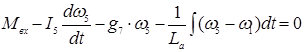8: (8)

узел 1: 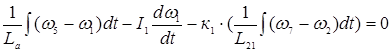(9)

2 подсистема:

узел 7: (10)

узел 2: 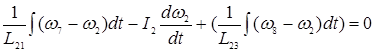(11)

узел 8: (12)

3 подсистема:

узел 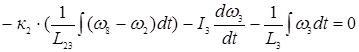3: (13)

4 подсистема:

узел 9: (14)

узел 10: 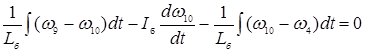(15)

узел 4: 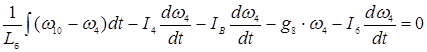(16)

Полученные уравнения следует привести к алгебраическому виду. Приведение осуществляют, используя следующие компонентные уравнения:

(17)

или (18)

(19)

Получим следующие уравнения:

1 подсистема:

узел 8: 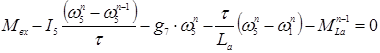(20)

узел 1: (21)

2 подсистема:

узел 7: 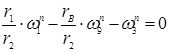(22)

узел 2: 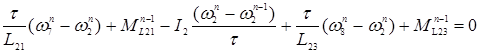(23)

узел 8: 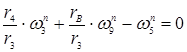(24)

3 подсистема:

Узел 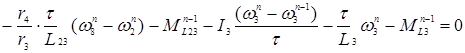(25)

4 подсистема:

узел 9: 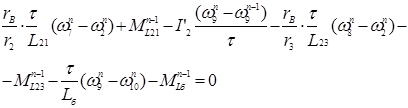(26)

узел 10: (27)

узел 4: (28)

 Скачать реферат